Developing a Python-Based Application for a Discrete-Time Population Dynamics Model
Main Article Content
Abstract
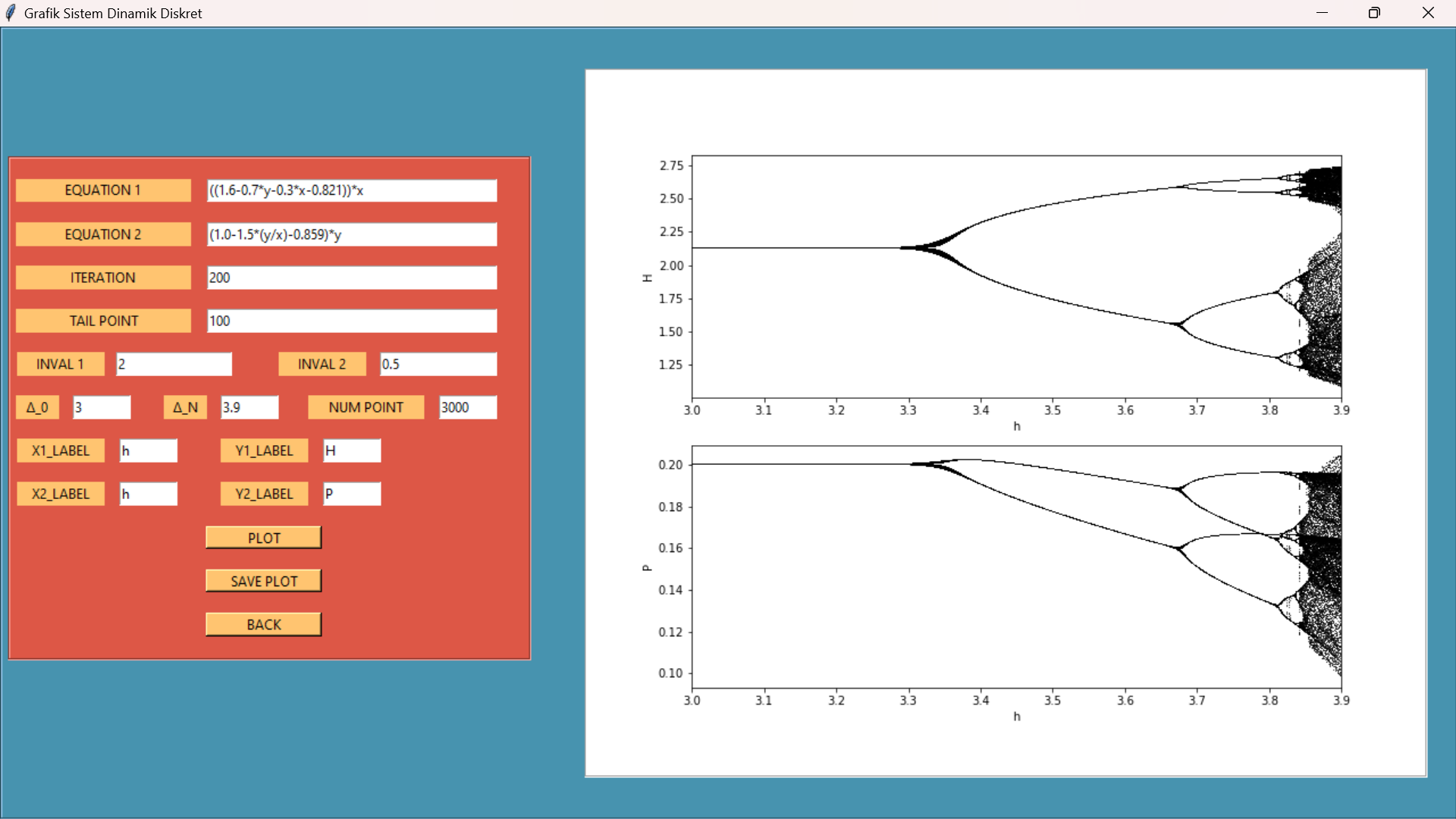
Difference equation is a type of equation in mathematics that is widely used to describe certain phenomena as time changes, one of which is in the field of population dynamics. In various studies, it is explained that solving complex population dynamics models is by using numerical simulations. Along with the development of technology, computational science is used to help solve mathematical problems that are difficult to solve analytically. One of them is to use a programming language, such as Python, to help present data in a graphical form. This research aims to develop an application that presents a computational solution to a difference equation using Python. The numerical results begin by entering the equation and variable values into the application, which then automatically generates a figure according to the entered equation. The figures generated in the application include one-dimensional and two-dimensional time series, as well as a Bifurcation diagram.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
References
Cushing JM. Difference equations as models of evolutionary population dynamics. Journal of Biological Dynamics. 2019;13(1):103-27.
Panigoro HS, Rahmi E. The Dynamics of a Discrete Fractional-Order Logistic Growth Model with Infectious Disease. Contemporary Mathematics and Applications (ConMathA). 2021;3(1):1.
Mokodompit R, Nurwan N, Rahmi E. Bifurkasi Periode Ganda dan Neimark-Sacker pada Model Diskret Leslie-Gower dengan Fungsi Respon Ratio-Dependent. Limits: Journal of Mathematics and Its Applications. 2020 jul;17(1):19.
Santra PK, Panigoro HS, Mahapatra GS. Complexity of a Discrete-Time Predator-Prey Model Involving Prey Refuge Proportional to Predator. Jambura Journal of Mathematics. 2022 jan;4(1):50-63.
Roza IZN, Pagalay U, Widayani H. Simulasi Model Diskrit Respon Sistem Imun pada Penyebaran Tumor Otak dengan Metode Beda Hingga Standar. Jurnal Riset Mahasiswa Matematika. 2021 dec;1(2):79-92.
Alya Rahmadani Harahap, Yahfizham Yahfizham. Algoritma Pemrograman Numerik Sebagai Solusi Efisien dari Permasalahan Matematika Kompleks. Jurnal Arjuna: Publikasi Ilmu Pendidikan, Bahasa dan Matematika. 2023;1(6):12-20.
Ra'yan I, Toaha S, Kusuma J. Dynamics Analysis of Predator-Prey Model with Double Allee Effects and Holling Type II Functional Response. Jurnal Matematika Statistika dan Komputasi. 2022;18(3):434-46.
Aini Q, Savitri D. Analisis Dinamik Model Mangsa Pemangsa Holling-Tanner dengan adanya Makanan Tambahan pada Pemangsa. MATHunesa: Jurnal Ilmiah Matematika. 2021 aug;9(2):418-30.
Resmawan R, Yahya L, Pakaya RS, Panigoro HS, Nuha AR. Analisis Dinamik Model Penyebaran COVID-19 dengan Vaksinasi. Jambura Journal of Biomathematics. 2022 jul;3(1):29-38.
Pratama DA, Bakar MA, Fadhilah N. Physical restriction neural networks with restarting strategy for solving mathematical model of thermal heat equation for early diagnose breast cancer. Results in Applied Mathematics. 2023;19:100384.
Guedes PFS, Lacerda MJ, Nepomuceno E. State-Feedback Control Design for Polynomial Discrete-Time Systems obtained via Second-Order Runge-Kutta Discretization. IFAC-PapersOnLine. 2024;58(5):13-9.
Elaydi SN. Discrete Chaos, Second Edition: With Applications in Science and Engineering. vol. 2007. Taylor and Francis; 2007.
Hanke JE, Wichern DW. Business Forecasting. Pearson Prentice Hall; 2005.
Hassona S, Marszalek W, Sadecki J. Time series classification and creation of 2D bifurcation diagrams in nonlinear dynamical systems using supervised machine learning methods. Applied Soft Computing. 2021;113:107874.
Qurban M, Khaliq A, Saqib M, Abdeljawad T. Stability, bifurcation, and control Modeling interaction of the predator-prey system with Alles effect. Ain Shams Engineering Journal. 2024; (September 2023):102631.
Purnomo AB, Prakoso MT, Evi M. Studi kasus ilmu komputer: Efektivitas perancangan model pembelajaran komputasi. Hexatech: Jurnal Ilmiah Teknik. 2022 aug;1(2):55-9.
Suharto A. Fundamental Bahasa Pemrograman Python. Eureka Media Aksara; 2023.
Dhruv AJ, Patel R, Doshi N. Python: The Most Advanced Programming Language for Computer Science Applications. Proceeding of the International Conference on Culture Heritage, Education, Sustuinable Tourism, and Innovation Technologies. 2022; (Cesit 2020):292-9.
Linge S, Langtangen HP. Programming for Computations - Python. 2nd ed. Barth TJ, Griebel M, Keyes DE, Nieminen RM, Roose D, Schlick T, editors. SpringerOpen; 2018.
Kasliono K, Suharmono E, Povi P, Meriani R, Candraningrum N. Analisis Regresi dan Korelasi untuk Proyeksi Produksi Minyak Bumi dan Gas Alam Indonesia menggunakan Bahasa Pemrograman Python. Jurnal Teknologi Informatika dan Komputer. 2023 sep;9(2):1297-313.
Moore AD. Python GUI Programming with Tkinter. second edi ed. Jain S, Katare N, Lucy W, Sonawane K, editors. Birmingham: Packt Publishing Ltd.; 2021.
Hunter J, Dale D, Firing E, Droettboom M. Matplotlib Release 1.5.1; 2016.
Wahid AA. Analisis Metode Waterfall Untuk Pengembangan Sistem Informasi. Jurnal Ilmu-ilmu Informatika dan Manajemen STMIK. 2020; (October):5.
Sidik ATR, Panigoro HS, Resmawan R, Rahmi E. The existence of Neimark-Sacker bifurcation on a discrete-time SIS-Epidemic model incorporating logistic growth and allee effect. Jambura Journal of Biomathematics. 2022;3(2):58-62.
Ernawati PD, Darti I. Stability analysis of the euler discretization for the harvesting Leslie-Gower predator-prey model. International Journal of Pure and Applied Mathematics. 2015;105(2):213-21.