Dynamics of Alcohol Consumption Model with Public Awareness and Saturated Incidence
Main Article Content
Abstract
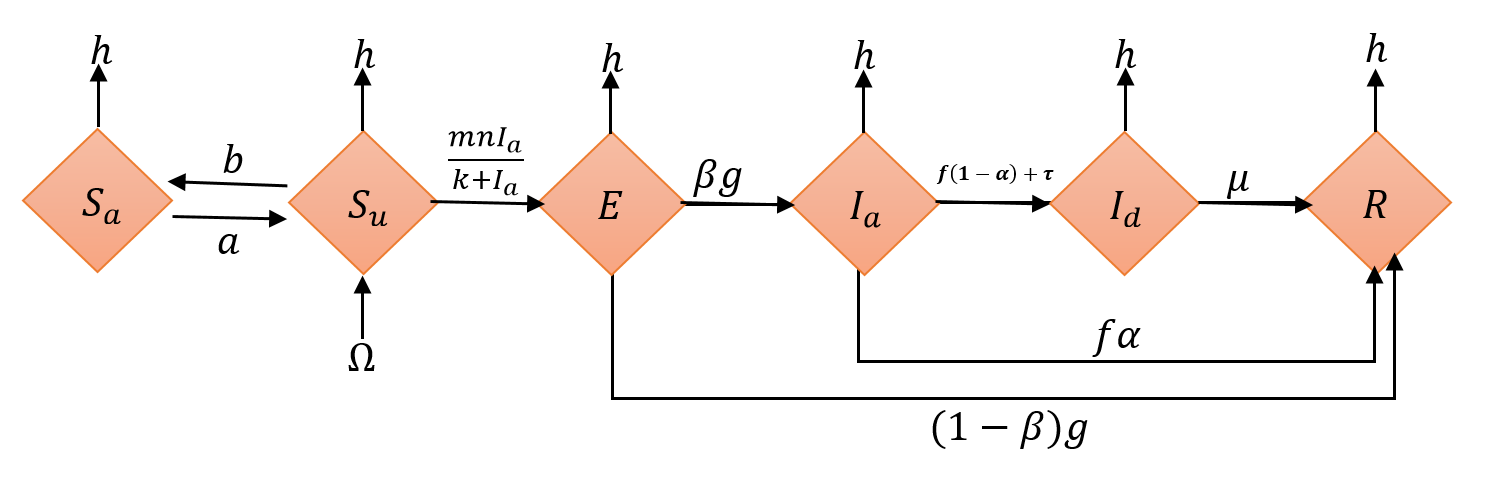
This article develops a mathematical model for studying the impact of public awareness and intervention strategies on alcohol consumption patterns. To protect populations from addiction, we are focusing on educational campaigns and interventions. Alcohol consumption cases decrease as the model variable awareness susceptible class is increased through awareness campaigns and interventions. The nonnegativity and boundedness of the model's solutions are analyzed. A qualitative analysis of the model's equilibrium points and the alcohol reproductive number, R0, was performed. Global stability was analyzed for alcohol consumption at the positive equilibrium point via a suitable Lyapunov function. When the alcohol reproductive number (R0) is less than one, the alcohol-free equilibrium is globally asymptotically stable; otherwise, it is unstable. Although educational campaigns protect vulnerable people, their impact on the model is substantial. The simulation shows that the intervention directly and drastically reduces the target alcoholic population.
Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
References
Elsonbaty A, Adel W, Aldurayhim A, El-Mesady A. Mathematical modeling and analysis of a novel monkeypox virus spread integrating imperfect vaccination and nonlinear incidence rates. Ain Shams Engineering Journal. 2024 Mar;15(3):102451.
Beay LK, Saija M. Dynamics of a stage–structure Leslie–Gower model with Michaelis–Menten type harvesting. AIP Conference Proceedings. 2022;020003.
Beay LK, Leleury ZA, Rijoly ME, Lesnussa YA, Wattimena AZ, Rahakbauw DL. A Stage-structure Leslie-Gower Model with Linear Harvesting and Disease in Predator. Jambura Journal of Biomathematics. 2023 Dec;4(2).
Peter OJ, Panigoro HS, Abidemi A, Ojo MM, Oguntolu FA. Mathematical Model of COVID-19 Pandemic with Double Dose Vaccination. Acta Biotheoretica. 2023 Jun;71(2):9.
Din A, Li Y. The extinction and persistence of a stochastic model of drinking alcohol. Results in Physics. 2021 Sep;28:104649.
Sher M, Shah K, Sarwar M, Alqudah MA, Abdeljawad T. Mathematical analysis of fractional order alcoholism model. Alexandria Engineering Journal. 2023 Sep;78:281–91.
Mayengo MM. Modeling the prevalence of alcoholism with compulsory isolation treatment facilities. Results in Physics. 2023 May;48:106428.
Sivashankar M, Boulaaras S, Sabarinathan S. Stability Analysis of Fractional-Order Nonlinear Alcohol Consumption Model and Numerical Simulation. Fractal and Fractional. 2025 Jan;9(2):61.
Basir FA, Nieto JJ, Raezah AA, Abraha T. Impact of local and global awareness campaigns on malaria transmission: A mathematical model with protected human class and optimal control approach. The European Physical Journal Plus. 2025 Mar;140(3):262.
Goswami NK, Olaniyi S, Abimbade SF, Chuma FM. A mathematical model for investigating the effect of media awareness programs on the spread of COVID-19 with optimal control. Healthcare Analytics. 2024 Jun;5:100300.
Ochieng FO. SEIRS model for malaria transmission dynamics incorporating seasonality and awareness campaign. Infectious Disease Modelling. 2024 Mar;9(1):84–102.
Mahdy AMS, Lotfy K, El-Bary AA. Use of optimal control in studying the dynamical behaviors of fractional financial awareness models. Soft Computing. 2022 Apr;26(7):3401–9.
Beay LK, Panigoro HS, Rahmi E, Savitri D. Modeling of Abstinence Behavior on the Electoral Lists with Awareness Campaigns and Argumentative Schemes. Communication in Biomathematical Sciences. 2024 Dec;7(2):219–31.
Ullah MA, Raza N. A simulation-based analysis of a novel HIV/AIDS transmission model with awareness and treatment. Nonlinear Dynamics. 2024 Dec;112(24):22529–48.
Ndii MZ, Beay LK, Anggriani N, Nukul KN, Djahi BS. Estimating the Time Reproduction Number in Kupang City Indonesia, 2016–2020, and Assessing the Effects of Vaccination and Different Wolbachia Strains on Dengue Transmission Dynamics. Mathematics. 2022 Jun;10(12):2075.
Sahusilawane ME, Ilwaru VYI, Lesnussa YA, Beay LK, Ojo MM, Permadi VA, et al. Stability Analysis Of A Mathematical Model Of Rabies Spread With Vaccination In Human And Dog Populations, Including Aware And Unaware Exposed Subpopulations. BAREKENG: Jurnal Ilmu Matematika dan Terapan. 2025 Apr;19(2):861–78.
Goyal A. Tobacco epidemics: Effect of marketing bans and awareness programs on its spread. Applied Mathematics and Computation. 2014 Nov;247:1030–51.
Ma SH, Huo HF, Meng XY. Modelling Alcoholism as a Contagious Disease: A Mathematical Model with Awareness Programs and Time Delay. Discrete Dynamics in Nature and Society. 2015;2015:1–13.
Ramamoorthi P, Muthukrishnan SK. Optimal control of alcoholism spreading through awareness over multiplex network. International Journal of Biomathematics. 2021 Aug;14(06):2150038.
Muchika CL, Apima S, Tireito F. Mathematical Modeling of Alcoholism Incorporating Media Awareness as an Intervention Strategy. Journal of Advances in Mathematics and Computer Science. 2022 Oct:1–15.
Kunwar LB, Verma VS. Mathematical Analysis of Alcoholism with Effect of Awareness through Media in Developing Countries. Engineering Letters. 2023;31(1):295–304.
Omame A, Abbas M. The stability analysis of a co-circulation model for COVID-19, dengue, and zika with nonlinear incidence rates and vaccination strategies. Healthcare Analytics. 2023 Nov;3:100151.
Ajbar A, Alqahtani RT, Boumaza M. Dynamics of an SIR-Based COVID-19 Model With Linear Incidence Rate, Nonlinear Removal Rate, and Public Awareness. Frontiers in Physics. 2021 May;9.
Beay LK, Anggriani N. Dynamical Analysis of a Modified Epidemic Model with Saturated Incidence Rate and Incomplete Treatment. Axioms. 2022 May;11(6):256.
Suryanto A, Kusumawinahyu WM, Darti I, Yanti I. Dynamically consistent discrete epidemic model with modified saturated incidence rate. Computational and Applied Mathematics. 2013 Jul;32(2):373–83.
Suryanto A, Darti I. On the nonstandard numerical discretization of SIR epidemic model with a saturated incidence rate and vaccination. AIMS Mathematics. 2021;6(1):141–55.